
Erst mit Hilfe der Quantentheorie kann man den Aufbau der Materie erklären. Die Quantentheorie ist, so könnte man sagen, die mathematische Formulierung des Welle-Teilchen-Dualismus. Auf mathematische Details kann hier nicht eingegangen werden, es sollen nur einige wichtige Grundprinzipien erläutert werden.
Wellen haben immer eine räumliche Ausdehnung; die elementaren Teilchen sind unteilbar, „punktförmig“. Dass diese beiden sich scheinbar widersprechenden Eigenschaften bei Materiewellen und auch beim Licht (Photonen!) miteinander vereinbar sind, ist schwer zu begreifen, aber alle experimentellen Daten deuten darauf hin.
Wir beschreiben also die Elektronen, die sich im Kraftfeld eines Atomkerns befinden (in dem fast die ganze Masse des Atoms vereint ist), als Wellen. Diese Wellenfunktionen sind selbst nicht beobachtbar, sondern Hilfsmittel, um beobachtbare Größen zu berechnen. Insbesondere erhält man aus dem Betragsquadrat der Wellenamplitude die Teilchendichte (Aufenthaltswahrscheinlichkeitsdichte).
Das allereinfachste Atom ist das Wasserstoffatom. Der Kern trägt eine positive Elementarladungeinheit und kann daher nur ein Elektron an sich binden. Dessen mögliche Wellenfunktionen lassen sich als Lösungen der Schrödingergleichung noch exakt bestimmen; der Lösungsweg und die Ergebnisse sind in den gängigen Lehrbüchern der Quantenmechanik zu finden. Die mathematischen Details sollen uns hier nicht beschäftigen, sondern es sollen einige allgemeine Eigenschaften von schwingenden Systemen, insbesondere stehenden Wellen, an einfachen Beispielen erläutert werden.
Die genaue Schwingungsform einer Gitarrensaite hängt davon ab, an welcher Stelle sie gezupft wurde. Man kann die Schwingung immer als Überlagerung von einfacheren Schwingungsformen beschreiben, die sich dadurch auszeichnen, dass alle Teile der Saite eine reine Sinusschwingung mit der gleichen Frequenz ausführen. Diese nennt man Eigenschwingungen, und die Überlagerung verschiedener Eigenschwingungen äußert sich akustisch als Überlagerung von Grundton und Obertönen.
Das Bild unten zeigt das Aussehen von Grund-, erster und zweiter Oberschwingung einer Saite. Die Bewegung erfolgt so schnell, dass das Auge sie nicht auflösen kann; man sieht eine Abfolge von Schwingungsbäuchen und -knoten.
An einfachen Saiten sind wichtige Eigenschaften der dreidimensionalen Wellen noch nicht zu beobachten; an
schwingenden Membranen kann man schon mehr sehen. Statt Knoten treten hier bei den höheren Eigenschwingungen Knotenlinien auf. Bei schwingenden Platten sind diese als Chladnische Klangfiguren aus Schulversuchen bekannt.
Wasserwellen sind zwar komplizierter zu beschreiben als die Wellen, die uns hier interessieren; aber wenn wir uns auf kleine Auslenkungen beschränken, dann stört das noch nicht. Wasserwellen haben den Vorteil, dass sie langsam sind und man daher die Wellenbewegung gut sieht. Die folgenden Bilder sind idealisiert und gewissermaßen in Zeitlupe zu sehen.
Die einfachste stehende Welle in einem Becher mit Wasser, die außerdem sehr leicht anzuregen ist, ist das Hin- und Herschwappen der Flüssigkeit. Dieses kann in beliebiger Richtung erfolgen und es gibt daher unendlich viele mögliche stehende Wellen dieser Form, alle mit der gleichen Frequenz.




| (a) | (b) | (c) | (d) |
Durch Doppelklicken auf eines der Bilder können Sie die Animation einschalten,
einfaches Klicken schaltet sie wieder aus. Wenn Sie auf die Buchstaben in Klammern unter den Bilden klicken, erscheint die Animation in einem getrennten Fenster.
Eine wesentliche Eigenschaft von Wellen ist, dass sie sich überlagern können. Durch eine Linearkombination, d.h. Überlagerung der zwei in Bild (a) und (b) gezeigten Wellen mit geeignet gewählten Gewichtsfaktoren, lassen sich alle anderen darstellen. Auch die in Bild (c) und (d) gezeigten im Gegenuhrzeigersinn und im Uhrzeigersinn umlaufenden Wellen lassen sich durch Superposition von Wellen (a) und (b) mit Phasenverschiebungen von plus oder minus 90º erzeugen. Es gibt daher nur zwei linear unabhängige Eigenschwingungen dieses Typs.
Die Wellenform in Bild (e) kann man anregen, indem man Tropfen in das Glas fallen lässt. Die Welle ist drehsymmetrisch und es gibt daher keine zweite mit anderer Orientierung. Die Welle in Bild (f) lässt sich durch leichtes Rütteln am Glas mit entsprechender Frequenz wieder in beliebiger Richtung anregen; ähnlich wie oben lässt sich jede dieser Wellen als Überlagerung aus zwei „Basiswellen“ darstellen, die die gleiche Form haben, aber gegeneinander um 45º verdreht sind. Ebenso lassen sich auch umlaufende Wellen wie (g) durch Überlagerung gewinnen. Der dunkle Punkt in der Mitte soll andeuten, dass sich dieser Punkt der Oberfläche in Ruhe befindet.
Als Illustration der Materiewelle des Elektrons im Wasserstoffatom werden nicht die Wellen selbst, sondern das Quadrat der lokalen Amplitude der Wellen dargestellt. Diese Größe ist identisch mit der Teilchendichte, und so ergibt sich das Bild einer „Elektronenwolke“, die hier weiß auf schwarzem Untergrund gezeigt wird. Jedes der gezeigten Wölkchen, auch wenn es aus mehreren Teilen besteht, enthält genau das eine Elektron des Wasserstoffatoms.
|
1s |
Im Zustand mit der niedrigsten Energie ist die Welle kugelsymmetrisch und hat keine Knotenfläche. Das Elektron hält sich ganz in der Nähe des Kerns auf. Maßstab: Die Bildbreite beträgt das sechzigfache des Bohrschen Radius, also 3.17 nm. Dieser Maßstab wird bei den folgenden Bildern beibehalten. |
|
2s |
2p | Zur nächsthöheren Energie gibt es zwei verschieden aussehende Zustände. Der eine ist kugelsymmetrisch und hat eine kugelförmige Knotenfläche, wo die Teilchendichte Null ist (linkes Bild), der andere ist rotationssymmetrisch um eine Symmetrieachse, deren Richtung im Raum beliebig ist. (Im Bild ist die Symmetrieachse vertikal.) Man kann aber jede dieser unendlich vielen verschiedenen Funktionen als Überlagerung von drei Basisfunktionen darstellen, deren Achsen man zweckmäßigerweise in Richtung der Koordinatenachsen wählt. |
Wir numerieren die Energieniveaus mit der „Hauptquantenzahl“ n. Die Nummer des Grundzustands ist n=1, die des ersten angeregten Zusrands n=2, und so weiter. Die Buchstaben s, p, d, f, die neben der Hauptquantenzahl unter den Bildchen stehen, sind historisch bedingt und leiten sich von Eigenschaften ab, die man anfangs bei den Zuständen vermutete (sharp, principal, diffuse, fundamental); hinter diesen Buchstaben verbirgt sich die Bahndrehimpuls-Quantenzahl l, und s bedeutet l = 0, p bedeutet l = 1, d steht für l = 2, f für l = 3, und dann geht es weiter mit dem Alphabet.
|
3s |
3p |
3d |
Das Kraftzentrum denken wir uns im Koordinatenursprung. Die x-Achse soll nach vorne aus der Bildschirmebene heraus zeigen, die y-Achse nach rechts und die z-Achse nach oben.
Es ist leicht, sich sechs verschiedene und im gewählten Koordinatensystem besonders einfach ausgerichtete 3d Elektronenwolken bzw. Wellenfunktionen vorzustellen: in dem oben gezeigten Fall liegen die Dichtemaxima in der y-z-Ebene zwischen den Koordinatenachsen, die x-y- und die x-z-Ebene sind Knotenflächen.
Denken wir uns das Wölkchen um 90º um die z-Achse gedreht, dann liegen die Maxima in der z-x-Ebene, das ist die zweite spezielle Lage, und in der dritten speziellen Lage liegen die Maxima in der x-y-Ebene.
|
| Als nächstes denken wir uns das 3d-Wölkchen oben um 45º um die x-Achse gedreht: dann erhalten wir die nebenstehende Dichteverteilung. Die Dichtemaxima liegen jetzt auf den Koordinatenachsen in der y-z-Ebene. Zwei weitere Zustände ergeben sich wieder durch Drehung um 90º um die z- bzw. y-Achse. |
Addiert man diese drei Ausdrücke, so ergibt sich als Summe Null, mit anderen Worten, die sechste der gefundenen Funktionen lässt sich als negative Summe der beiden anderen schreiben und ist somit überzählig.
|
3d (m=0) | Es ist üblich, die Differenz der beiden oberen Zeilen (geteilt durch die Wurzel aus 3; die zugehörige, um die vertikale z-Achse drehsymmetrische Wolke sehen Sie im nebenstehenden Bild), und die Funktion in der dritten Zeile als Basisfunktionen beizubehalten. |
Die Schrödingergleichung liefert gleichzeitig die Energien und die Wellenfunktionen der möglichen Zustände eines Elektrons im Coulombpotential (Wasserstoffatom und wasserstoffähnliche Ionen). Der Nullpunkt der Energieskala wird so gewählt, dass ein ruhendes, unendlich weit vom Kern entferntes Elektron die Energie Null hat. Die Energie des Atoms im Grundzustand ist dann negativ und dem Betrag nach gleich der Energie, die man benötigt um das Atom zu ionisieren, d.h. das Elektron vom Kern zu trennen.
 | Energieniveauschema des Wasserstoffatoms. Die Niveaus sind für die verschiedenen Bahndrehimpulse getrennt gezeichnet. Die Zustände sind durch die Hauptquantenzahl n und die Bahndrehimpulsquantenzahl gekennzeichnet, wobei die Buchstaben s, p, d, f, g, h der Reihe nach für l = 0, 1, 2, 3, 4, 5 stehen. |
Unter Absorption von elektromagnetischer Strahlung oder durch Stöße mit energiereichen Teilchen (z.B. bei hoher Temperatur) können Übergänge von niedrigen in höhere Energieniveaus stattfinden, und umgekehrt kann der Übergang von höherenergetischen Zuständen in niedrigere unter Emission von elektromagnetischer Strahlung erfolgen, aber die Energie kann auch wieder beim Zusammenstoß mit anderen Atomen oder Molekülen abgegeben werden. Die Energie der emittierten Photonen ist die Energiedifferenz zwischen Anfangs- und Endzustand.
Für Photonen gilt die grundlegende quantenmechanische Beziehung zwischen Energie und Frequenz ν (h ist das Plancksche Wirkungsquantum)

|
3d |
Überlagerung von 2p und 3d |
2p |
Das nach dem Wasserstoff nächst einfachste Atom ist das Heliumatom. Es besteht aus einem mit zwei Elementarladungen elektrisch positiv geladenen Kern und zwei Elektronen. Eine exakte analytische Lösung der Schrödingergleichung ist nicht mehr möglich, man ist auf Näherungsverfahren und numerische Methoden angewiesen.
In einer genäherten Beschreibung eines Atoms mit mehr als einem Elektron ersetzt man die Wechselwirkung der Elektronen untereinander durch ein statisches elektrisches Potential. Ein Elektron, das sich weit weg vom Kern befindet, „spürt“ die Anziehungskraft des Kerns und die Abstoßung durch die übrigen Elektronen; durch diese wird die Kernladung abgeschirmt. Je näher das Elektron dem Kern kommt, desto geringer wird die Abschirmung. Das effektive Potential für ein Elektron in einem neutralen Atom nähert sich für große Abstände dem Coulombpotential einer einzigen Elementarladung an, aber für Abstände, die nach Null gehen, wirkt die volle Kernladung.
Die Veränderung des Potentials wirkt sich auf die Wellenfunktionen und damit auch auf die Dichteverteilungen (Elektronenwolken) aus, aber das qualitative Erscheinungsbild bleibt erhalten, insbesondere die Symmetrien und die Anordnung der Knotenflächen.
|
1s |
Hier sehen Sie noch einmal die Dichteverteilung des Elektrons in einigen ausgewählten Eigenzuständen des Wasserstoffatoms, alle im gleichen Maßstab gezeichnet (Bildbreite jeweils 3.17 nm). | ||
|
2s |
2p |
|
3s |
3p |
3d |
3d (m=0) | ||
|
4s |
4p |
4d |
4d (m=0) |
4f |
4f (m=0) |
Der Sachverhalt, dass Zustände mit gleicher Hauptquantenzahl, aber verschiedenem Bahndrehimpuls die gleiche Energie haben, ist eine Besonderheit des Coulombpotentials. Wenn wir uns ein effektives Potential vorstellen, das außen dem Coulombpotential einer positiven Elementarladung ähnelt, in der Nähe des Kerns aber stärker anziehend ist, dann werden das die Elektronen in s-Zuständen am stärksten spüren, denn sie haben am Ort des Kerns ihre höchste Dichte. Von den Zuständen mit gleicher Hauptquantenuahl n, die im Coulombpotential alle die gleiche Energie haben, werden die mit l = 0 stärker abgesenkt als die mit l = 1, die wieder stärker als die mit l = 2 u.s.w., denn je größer l ist, desto größeren Abstand halten die Elektronenwölkchen vom Kern, wie man an den obigen Bildchen sieht.
Wenn die Energieniveaus sich aufspalten, ist unsere vorläufige Definition der Hauptquantenzahl als Nummer des Energieniveaus nicht mehr brauchbar. Sei nr die Zahl der kugelförmigen Knotenflächen, l die Bahndrehimpulsquantenzahl, dann definiert man n durch
Im Grundzustand des Heliumatoms besetzen beide Elektronen den energetisch niedrigsten Einteilchenzustand 1s, dafür benutzt man die Notation 1s2.
Man könnte erwarten, dass das nächst kompliziertere Atom, Lithium mit einem dreifach positiv geladenen Kern, die Elektronenkonfiguration 1s3 hat. Aber das stimmt nicht. Die experimentelle Information, die man aus den Spektren gewinnt, ist, dass in das niedrigste Niveau nur zwei Elektronen passen, das dritte muss mit dem nächsthöheren vorlieb nehmen, die Elektronenkonfiguration von Lithium ist daher 1s22s.
Man kann das Periodensystem der chemischen Elemente nur verstehen, wenn man annimmt, dass jede durch die Quantenzahlen n und l und ihre Orientierung im Raum gekennzeichnete Wellenform von höchstens zwei Elektronen eingenommen werden kann. Diese zwei Elektronen müssen sich, wie man herausgefunden hat, in einer weiteren Quantenzahl (Spinquantenzahl) unterscheiden, die nur zwei Werte, 1/2 und −1/2 annehmen kann. (Darauf will ich zunächst nicht eingehen.) Es gilt also das Pauli-Prinzip (oder Pauli-Verbot; Wolfgang Pauli 1924), das besagt, dass die Zustände von zwei Elektronen am gleichen Ort niemals in allen Quantenzahlen übereinstimmen dürfen.
Es ist daher wichtig, zu wissen, wieviele Orientierungen es zu einer vorgegebenen Wellenform gibt. Die s-Wellen sind kugelsymmetrisch, daher gibt es zu jeder Hauptquantenzahl nur eine. Wir haben uns überlegt, dass man jede in beliebiger Richtung schwingende p-Welle als Überlagerung aus drei Basis-Wellen erzeugen kann, es gibt daher drei unabhängige p-Wellen, die man in x-, y- und z-Richtung wählen kann. Für die d-Wellen (l=2) haben wir fünf unabhängige Grundformen gefunden, und es gilt allgemein, dass zu jeder Bahndrehimpuls-Quantenzahl l genau 2l + 1 verschiedene Orientierungen im Raum möglich sind, die für freie Atome meist durch die sogenannte Magnetquantenzahl m angegeben werden, welche ganzzahlige Werte zwischen −l und l annehmen kann.
Betrachtet man einen mehrfach geladenen Kern und denkt sich ein Elektron nach dem anderen in das jeweils noch zugängliche niedrigstmögliche Niveau „eingefüllt“, so ergibt sich folgende Reihenfolge:
Als Beispiel die Elektronenkonfiguration von Molybdän:
An den oben gezeigten Bildchen der Dichteverteilungen sieht man, dass deren räumliche Ausdehnung mit der Hauptquantenzahl n stark zunimmt. Dies rechtfertigt den Ausdruck „Schale“ für die Gesamtheit der Zustände zum gleichen Wert von n, obwohl diese Schalen nicht säuberlich voneinander getrennt sind. Die Gesamtheit der Zustände mit gleichem n und l heißen Unterschalen. Eine vollgefüllte Unterschale ist kugelsymmetrisch; eine vollgefüllte Schale ist besonders stabil und daher chemisch inert; die möglichen Wechselwirkungen eines Atoms mit seinen Nachbarn – also die chemischen Eigenschaften – werden in erster Linie von den Elektronen, deren Dichteverteilungen am weitesten nach außen reichen, bestimmt. So ergibt sich aus der oben angegebenen Reihenfolge der Schalenbesetzung und dem Sachverhalt, dass sich die Symmetrieeigenschaften der Zustände wiederholen, das Periodensystem der Elemente.
Wasserstoff ist ein farbloses Gas; unter „normalen“ Bedingungen sind die Atome paarweise zu Molekülen H2 gebunden und man bemerkt nichts von der Möglichkeit, dass Licht emittiert und absorbiert werden kann. Luft (Stickstoff und Sauerstoff) und die Edelgase sind farblos, und ähnliches gilt für viele andere Substanzen. Damit Spektrallinien in Emission oder auch in Absorption beobachtet werden können, müssen die Atome erst einmal durch Energiezufuhr in die angeregten Zustände gebracht werden.
In einer Gasentladungsröhre werden die Moleküle durch Stöße mit Elektronen und Ionen aufgebrochen, die Atome in angeregte Zustände versetzt, und dann ist sowohl die Emission (Leuchten) als auch die Absorption beobachtbar.
Hohe Temperaturen bewirken das gleiche: In der Sonne gibt es atomaren Wasserstoff in angeregten Zuständen, und man kann im Sonnenspektrum die Absorptionslinien des Wasserstoffs als dunkle Linien beobachten.
Die Temperaturen in der Flamme eines Bunsenbrenners reichen aus, um Moleküle zu spalten und Atome zu ionisieren, die dann nach der Rekombination ihre Energie durch Emission von Lichtquanten wieder abgeben. Mit Spuren von Alkali- oder Erdalkalimetallen (aber auch anderen Substanzen) kann man die Flamme färben, dies wird für Feuerwerkskörper ausgenutzt; die Flammenfärbung wird auch zum Nachweis dieser Substanzen verwendet, siehe z.B. die Wikipedia unter Flammenfärbung. Es ergibt
|
|
|
|
| ||||||||||||||||
| Lithium | Bor | Kupfer | Calcium |
Die nach dem Wasserstoffspektrum am einfachsten zu deutenden Spektren findet man bei den Alkalimetallen: sie besitzen ein einzelnes, relativ schwach gebundenes Elektron außerhalb der stabilen, kugelsymmetrischen abgeschlossenen Schalen. Man nennt dieses das Leuchtelektron, denn seine Übergänge zwischen den nächstliegenden Anregungszuständen und dem Grundzustand sind für den sichtbaren Teil der emittierten Strahlung verantwortlich.
Das Spektrum des Natriums wird durch eine Linie bei 589 nm Wellenlänge dominiert, die beim Übergang vom 3p-Zustand in den 3s-Zustand emittiert wird. (Infolge der Feinstrukturaufspaltung des p-Zustandes, die hier nicht behandelt wurde, handelt es sich tatsächlich um ein Dublett, d.h. zwei sehr nahe beieinanderliegende Linien.)



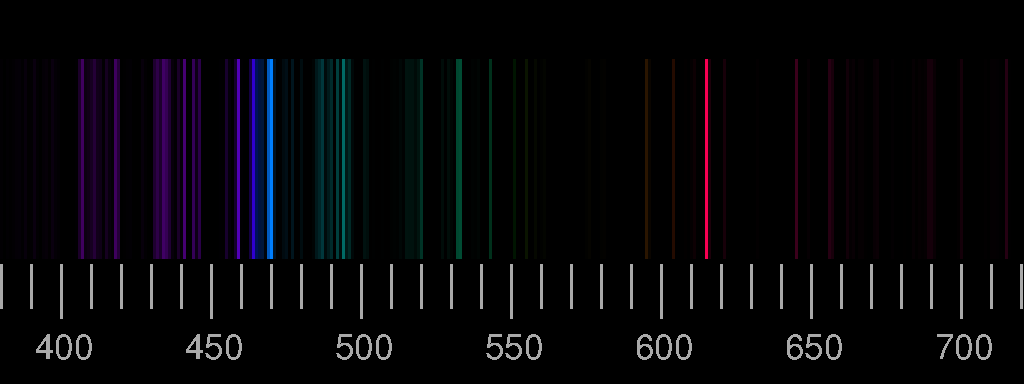
Oben das Linienspektrum von Stickstoff, unten das von Sauerstoff. Die Bilder basieren auf den Saha-LTE (local thermodynamic equilibrium) Spektren der NIST Atomic Spectra Database mit den Parametern Temperatur 12 eV, Elektronendichte 2.0×1022 cm−3.
Reale Spektren können sich von diesen synthetischen deutlich unterscheiden, indem Linien, die hier gezeigt werden, dort nicht auftreten, oder aber dass Linien zu sehen sind, die in den Bildern oben nicht vorhanden sind. Ein Beispiel ist das Blitz-Spektrum.
Die relativen Intensitäten der Linien hängen von den Bedingungen bei der Anregung und Lichtemission ab. Nur im Idealfall einer dünnen Plasmaschicht im thermodynamischen Gleichgewicht sind Temperatur und Elektronendichte allein entscheidend.
Ein elektrischer Funken in Luft, der mit einer kleinen Influenzmaschine erzeugt wurde, fotografiert durch ein Beugungsgitter. Der kontinuierliche Untergrund zusätzlich zu den diskreten „Linien“ rührt von der Lichtemission beim Einfang von freien Elektronen durch die Ionen her.
Auch die Linien, die eigentlich violett sein sollten, erscheinen auf diesem Foto blau, die gelbe Stickstofflinie grün und die orange rot. Spektralfarben lassen sich fotografisch (und auch sonst) nicht getreu reproduzieren. Darauf wurde bei der Besprechung von Prismenversuchen schon hingewiesen. Klicken Sie auf das obige Spektrum um ein Bild zu sehen, das durch Nachbearbeitung dem visuellen Eindruck etwas angenähert wurde!
Wir werden weiter unten bei der Besprechung des Polarlichts auf Spektrallinien des Sauerstoffs stoßen, das soll hier vorbereitet werden.
Die an Polarlicht am häufigsten zu beobachtenden Spektrallinien sind Linien des atomaren Sauerstoffs mit Wellenlängen von 558 nm (grün) und 630 nm (rot). In dem oben gezeigten Spektrum sind diese Linien überhaupt nicht vorhanden!
Werfen wir einen Blick auf die Elektronenkonfiguration des Sauerstoffs: Der Kern ist achtfach positiv geladen, denkt man sich die Elektronen sukzessive in die jeweils niedrigsten möglichen Zustände eingefüllt, ergibt sich folgende Konfigutation:
Die äußeren vier 2p-Elektronen können sich auf sechs mögliche Einteilchenzustände verteilen. Wäre keine Wechselwirkung zwischen diesen Elektronen vorhanden, dann wären alle fünfzehn Möglichkeiten energetisch gleich. Aber die Elektronen stoßen sich wegen ihrer gleichnamigen Ladungen gegenseitig ab.
Elektronen mit gleicher Spinausrichtung können sich schon aufgrund des Pauli-Prinzips nicht zu nahe kommen, daher ist Parallelausrichtung der Spins energetisch günstig.
Je größer der Gesamt-Bahndrehimpuls ist, desto geringer ist die Überlappung der Dichteverteilungen der einzelnen Elektronen. So ergibt sich die Aufspaltung der Niveaus nach dem Gesamt-Bahndrehimpuls („Grobstruktur“). Darüber hinaus besteht auch Wechselwirkung zwischen Spin- und Bahndrehimpuls, was zu einer weiteren Niveauaufspaltung je nach Gesamtdrehumpuls führt („Feinstruktur“). Für die leichteren Elemente ist die Spin-Bahn-Wechselwirkung gering.
Solange keine Richtung im Raum ausgezeichnet ist, ist der Gesamtdrehimpuls erhalten und die Zustände können durch die Quantenzahlen des Drehimpulses J gekennzeichnet werden.
| Konfiguration | Term | J | Niveau (cm−1) |
| 1s2 2s2 2p4 | 3P | 2 | 0.000 |
| 1 | 158.265 | ||
| 0 | 226.977 | ||
| 1s2 2s2 2p4 | 1D | 2 | 15867.862 |
| 1s2 2s2 2p4 | 1S | 0 | 33792.583 |
| 1s2 2s2 2p3(4S)3s | 5S | 2 | 73768.200 |
| . . . |
Man erhält daraus für den Übergang 1S→1D die Wellenlänge 558 nm – das ist die grüne Linie, und für den Übergang 1D→3P die Wellenlänge 630 nm, die rote Sauerstofflinie des Polarlichtes. Aber warum sind diese Linien unter Laborbedingungen nicht zu sehen?
Große Übergangswahrscheinlichkeiten beobachtet man nur bei Übergängen, die den Auswahlregeln ΔL = ±1, ΔS = 0, ΔJ = 0, ±1 (keine J=0 → J=0 Übergänge) genügen, dann ist elektrische Dipolstrahlung möglich. Übergänge, die diese Auswahlregeln nicht erfüllen, werden seit der Frühzeit der Atomphysik als „verboten“ bezeichnet, weil die Übergangswahrscheinlichkeiten so gering sind, dass sie oft überhaupt nicht beobachtet werden können. Es wären elektrische Quadrupol- oder magnetische Dipol- etc. -Übergänge möglich, aber die angeregten Atome verlieren ihre Energie durch Stöße viel rascher, als sie sie abstrahlen können.
Die beiden hier betrachteten Übergänge sind in diesem Sinne „verboten“. 1S→1D ist ein elektrischer Quadrupolübergang; bei 1D→3P ist ΔS ≠ 0, es muss ein Spin umklappen.
(Bei der Behandlung der Farbstoffe wird etwas genauer auf die Emissions- und Absorptionswahrscheinlichkeiten eingegangen.)
Wie eingangs schon erwähnt, ist von einzelnen Atomen ausgesandtes Licht ohne menschliches Zutun in der Natur selten zu beobachten. Bis auf Blitze und Polarlichter gibt es kaum natürliche irdische Beispiele. Dafür sind diese aber, wenn man sie zu Gesicht bekommt, umso eindrucksvoller:
Ursache der Polarlichterscheinungen sind geladene Teilchen (Protonen und Elektronen), die von der Sonne kommen („Sonnenwind“ wechselnder Stärke) und vom Magnetfeld der Erde abgelenkt werden. Die Vorgänge sind im einzelnen sehr kompliziert, siehe die Atmospheric Optics und die COMET® (Meteorology Education and Training) Webseiten.
Links: Nordlicht am 22.10.2001, 22:00 UT, aufgenommen nördlich von Wiesbaden
.
Rechts: Nordlicht am 30.10.2003, 19:57 Uhr UT, aufgenommen in der Nähe von Wolfsheim (Rheinhessen) .
Beide Fotos: © Ulrich Rieth; Wiedergabe mit freundlicher Genehmigung.
Ströme energiereicher geladener Teilchen fließen in großer Höhe entlang der „Magnetfeldlinien“, wobei sich die einzelnen Teilchen auf Wendelbahnen bewegen. Die Teilchen kommen in Polnähe der Erdoberfläche am nächsten. Ihre Energie wird in Stößen auf die Teilchen der oberen Atmosphäre übertragen und von diesen in Form von Licht wieder abgegeben. Das Polarlicht entsteht in Höhen oberhalb von ca. 100 km bis etwa 200 km; bei starker Sonnenaktivität kann es auch noch viel höher entstehen und dann auch noch in mittleren Breiten zu sehen sein. Die Zusammensetzung der hohen Atmosphäre ist deutlich verschieden von den erdnahen Schichten: molekularer Stickstoff und atomarer Sauerstoff überwiegen alle anderen Teilchenarten.
Die rote Linie des Sauerstoffs (630 nm) dominiert in großer Höhe, tritt aber unterhalb 150 km nicht mehr in Erscheinung, weil die angeregten Sauerstoffatome im 1D-Zustand ihre Energie dort durch Stöße mit Stickstoffmolekülen viel schneller verlieren, als sie sie abstrahlen können. Die überwiegend grüne Farbe des Polarlichts unterhalb 150 km Höhe wird von der Spektrallinie des Sauerstoffs bei 558 nm hervorgerufen. Sie tritt in größerer Höhe nicht auf, weil der 1S-Zustand durch Stöße von Sauerstoffatomen im Grundzustand mit Elektronen oder Protonen nicht erreicht wird. Die Meinung ist, dass dieser Zustand bevölkert wird, indem angeregte Stickstoffmoleküle ihre Energie auf den Sauerstoff übertragen und dabei dessen Drehimpuls aufnehmen:


|
| Weitaus häufiger als die natürlichen Erscheinungen kann man – zumindest in der Stadt – künstlich angeregte atomare Lichtemission beobachten. Hier nur als Beispiel eine mit Neon gefüllte Gasentladungsröhre vor einer schwarzen Wand. (Diese und die nächste Aufnahme entstand im Universum® Bremen.) |
| Plasmalampen, erfunden von Nicola Tesla, wurden als dekorative Objekte, „Plasmasphären“, „Plasmakugeln“, von Bill Parker wiedererfunden. Sie enthalten ein verdünntes Edelgas oder Edelgas-Gemisch (ca. 2 bis 10 Torr); die Energiezufuhr zur Anregung der Atome erfolgt durch das Anlegen einer hochfrequenten Hochspannung (ca. 2 kV oder mehr je nach Größe, ca. 10–40 kHz). Die links abgebildete Kugel dürfte mit einem Neon–Xenon-Gemisch gefüllt sein (95% Ne, 5% Xe ist gebräuchlich), andere Gasgemische produzieren andersfarbige Lichtfäden.
|
Es wurde schon erwähnt, dass unter normalen irdischen Bedingungen nur bei den Edelgasen einzelne freie Atome vorhanden sind. Bei allen anderen Elementen können sich Verbindungen gleicher oder verschiedener Atome – Moleküle – bilden, deren Energie niedriger als die der freien Atome ist. Es soll hier nicht die Theorie der chemischen Bindung ausgebreitet werden; es soll nur daran erinnert werden, dass in Molekülen die am losesten gebundenen Elektronen der das Molekül aufbauenden Atome in größeren Molekülorbitalen energetisch günstigere Zustände einnehmen können, was dann zur chemischen Bindung führt.
Im allgemeinen ergibt sich bei der Verbindung verschiedener Elemente eine unsymmetrische Ladungsverteilung im Molekül und ein daraus resultierendes Dipolmoment, aufgrund dessen sich die Moleküle anziehen und die Tendenz haben, zu kondensieren, d.h. eine Flüssigkeit oder einen Festkörper zu bilden.
Kleine Moleküle aus den leichteren Elementen sind farblos. Ähnlich wie die sie aufbauenden Atome können sie kein sichtbares Licht absorbieren; erst im Ultraviolett haben die Photonen genügend Energie, um elektronische Anregungen im Molekül anzuregen. Die Schwingungen der Moleküle führen zu Absorption und Emission im infraroten Bereich und verursachen allenfalls sehr schwache Farbe wie beim Wasser.
Den stark farbigen größeren Molekülen ist ein eigenes Kapitel „Farbstoffe“ gewidmet; die Farbigkeit von Mineralien wird in dem Abschnitt über farbige Kristalle, Mineralien und Pigmente behandelt.
Zurück zur Übersicht: Wie kommt Farbe zustande?
Weiter: Feuer und Glut